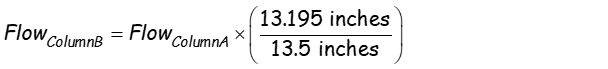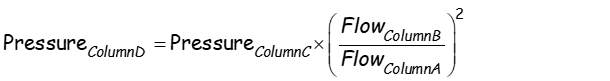The Affinity Laws
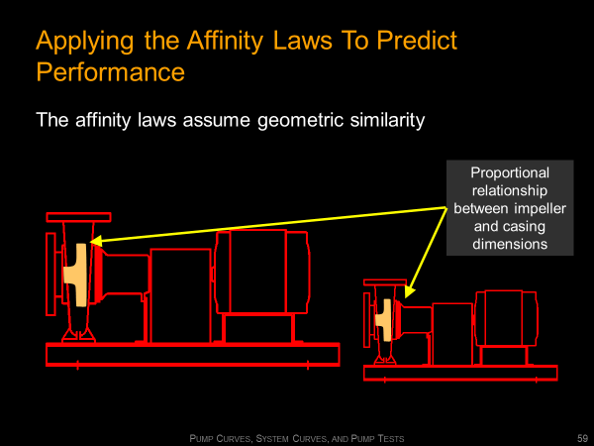
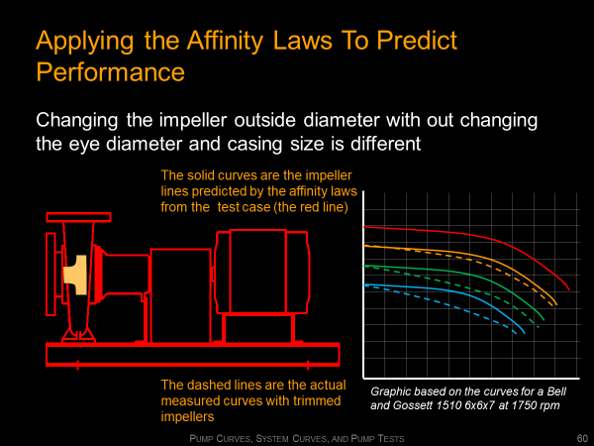
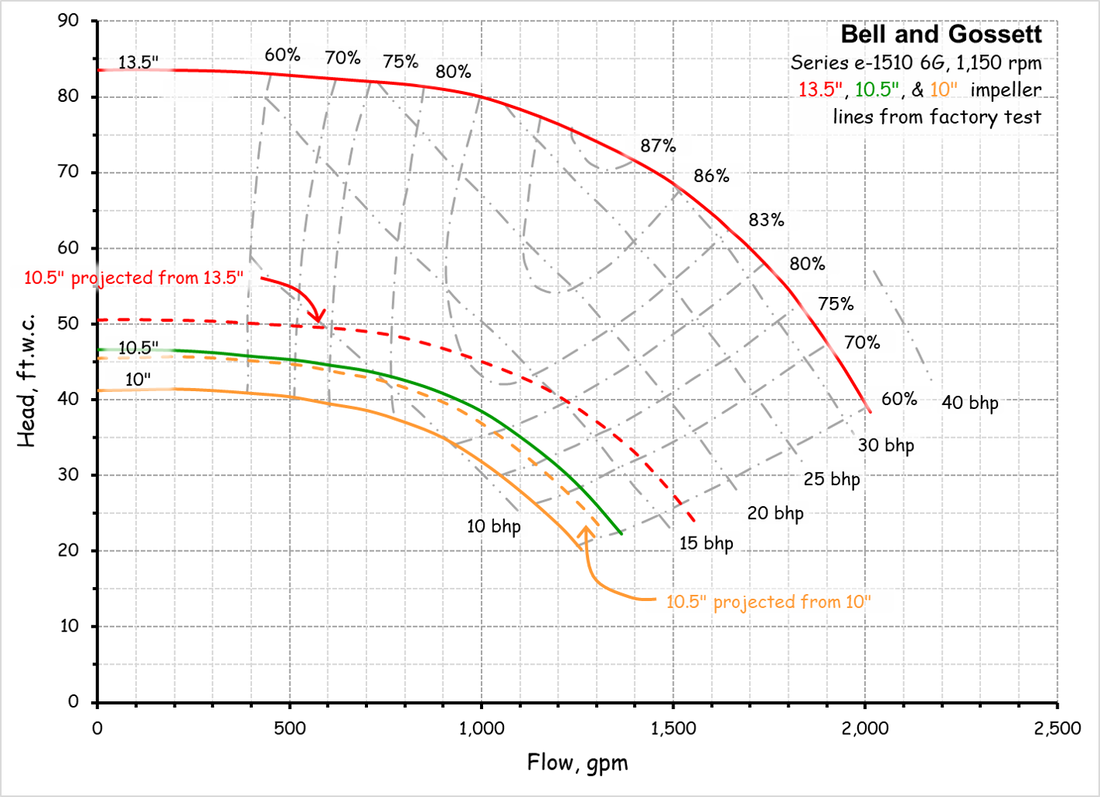
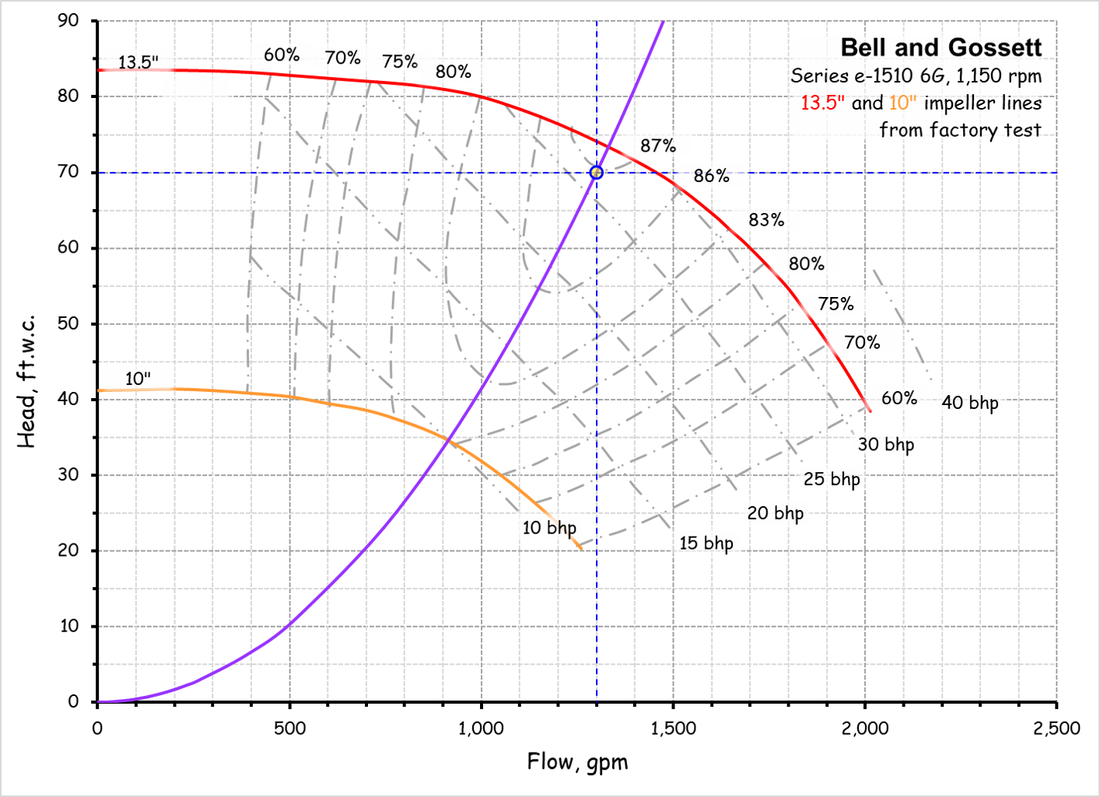
This page provides information and resources regarding the affinity laws that are used to project new performance points and curves for a pump or fan given a known performance point or curve.   In general, the affinity laws project the new operating point(s) by moving up and down a system curve.  That means the affinity laws can only be applied to a fixed system, which is an important constraint to recognize if you are going to use them.

For each of the laws listed below, you will find an explanation of how to apply them along with the equations from Mathtype in .wmf and .pdf form so you can document your math when you apply the concepts in a spreadsheet, which I believe is a professional and important thing to do.  If you follow the link above, in addition to explaining my philosophy on this, it will also explain how you can use the equation files.

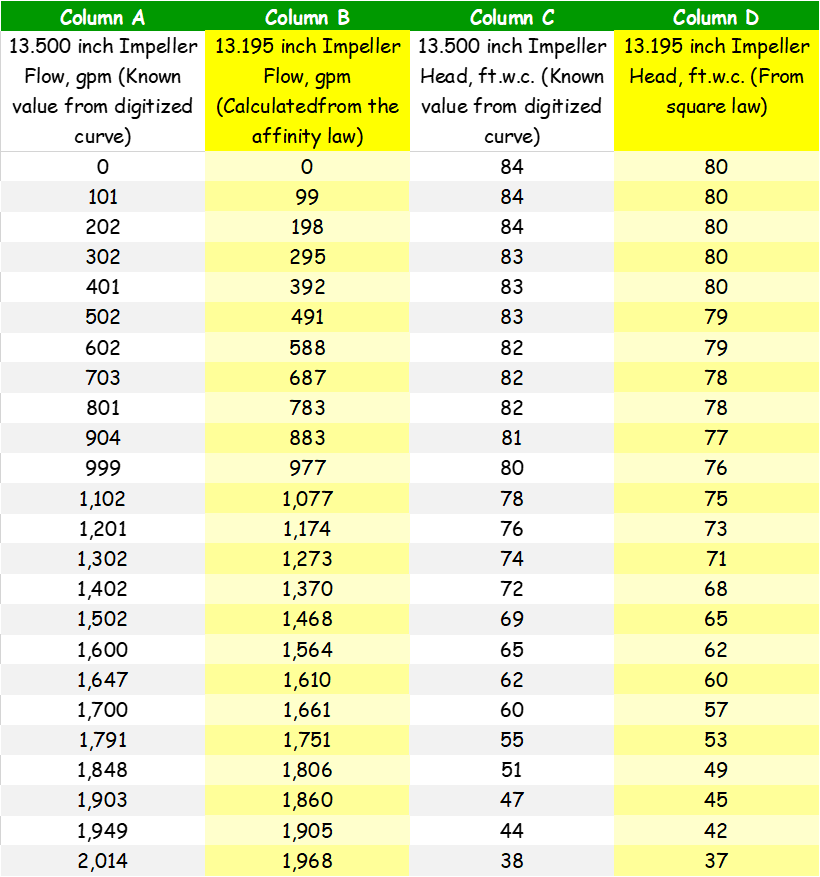
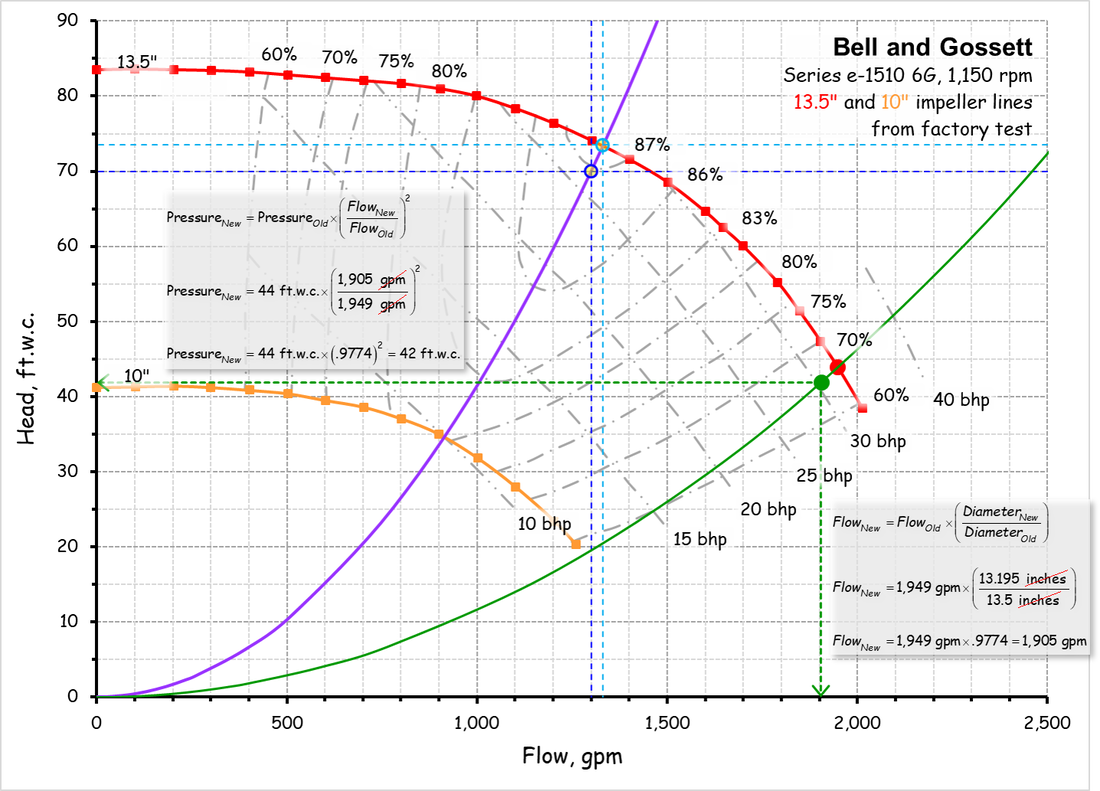
I have also included the spreadsheets that I used to generate the pump curve illustrations.   They are based on the Plot Digitizer Pump Curve Example spreadsheet and illustrate how you can don the affinity law math in the spreadsheet and plot the result on the pump curve.

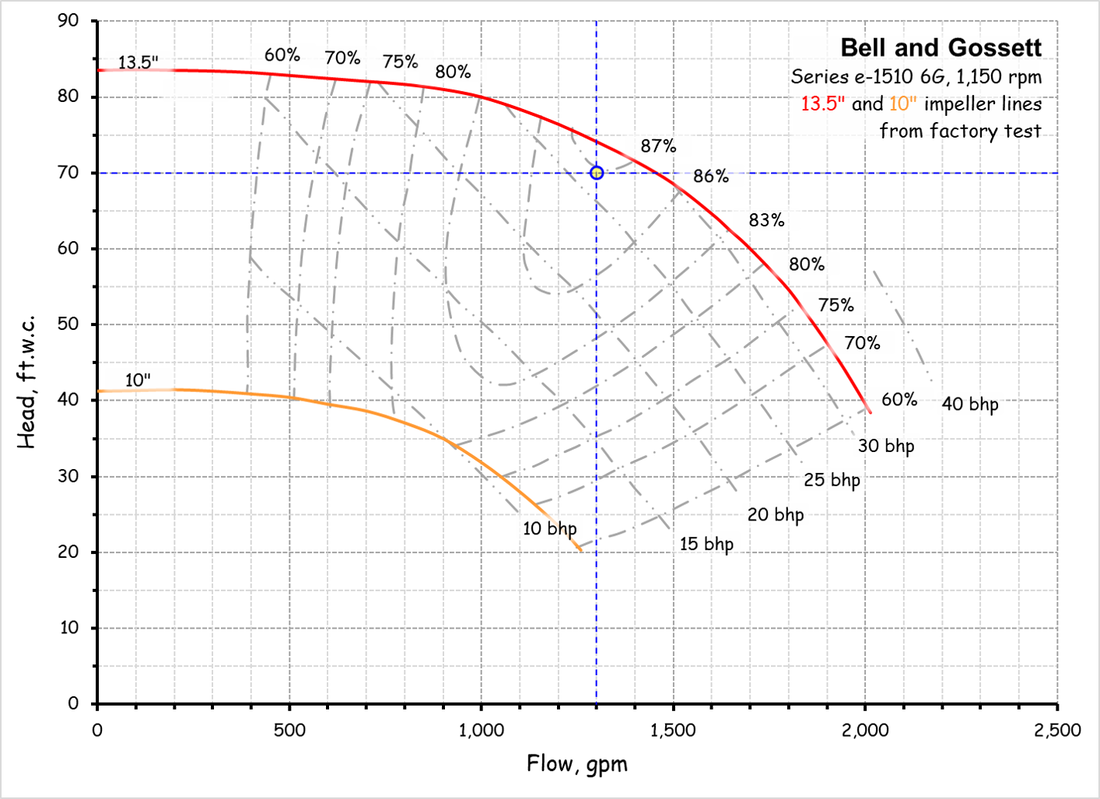
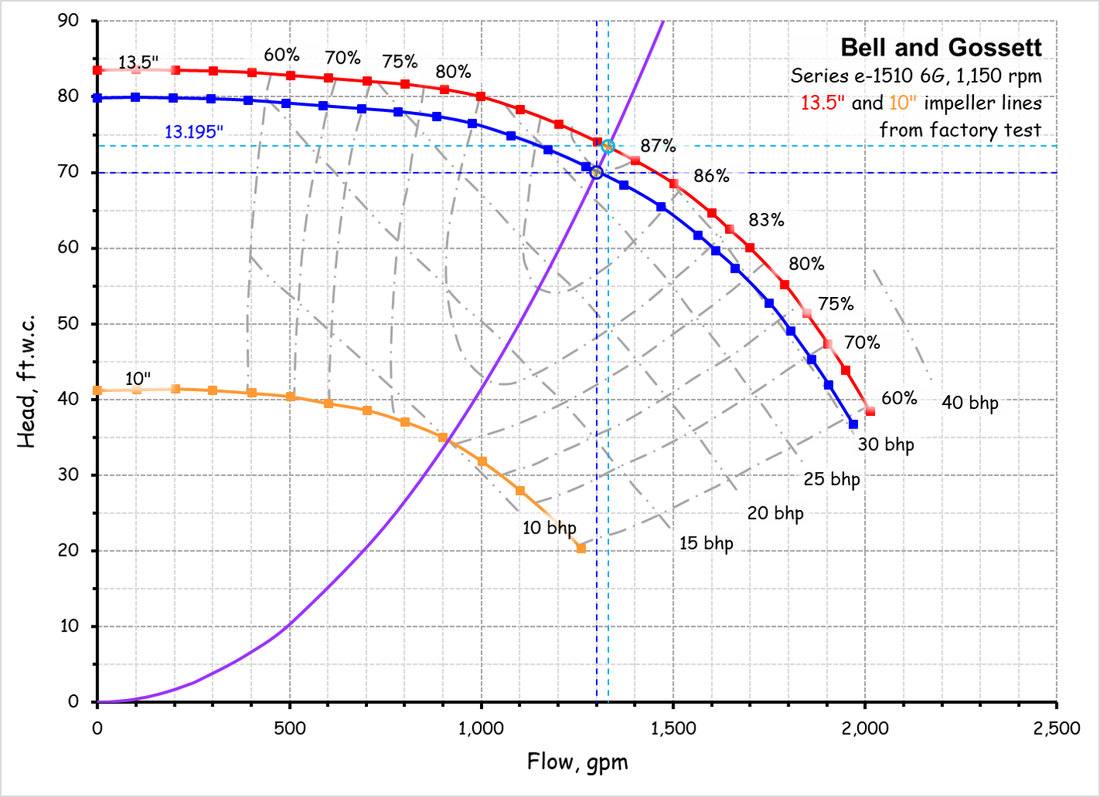
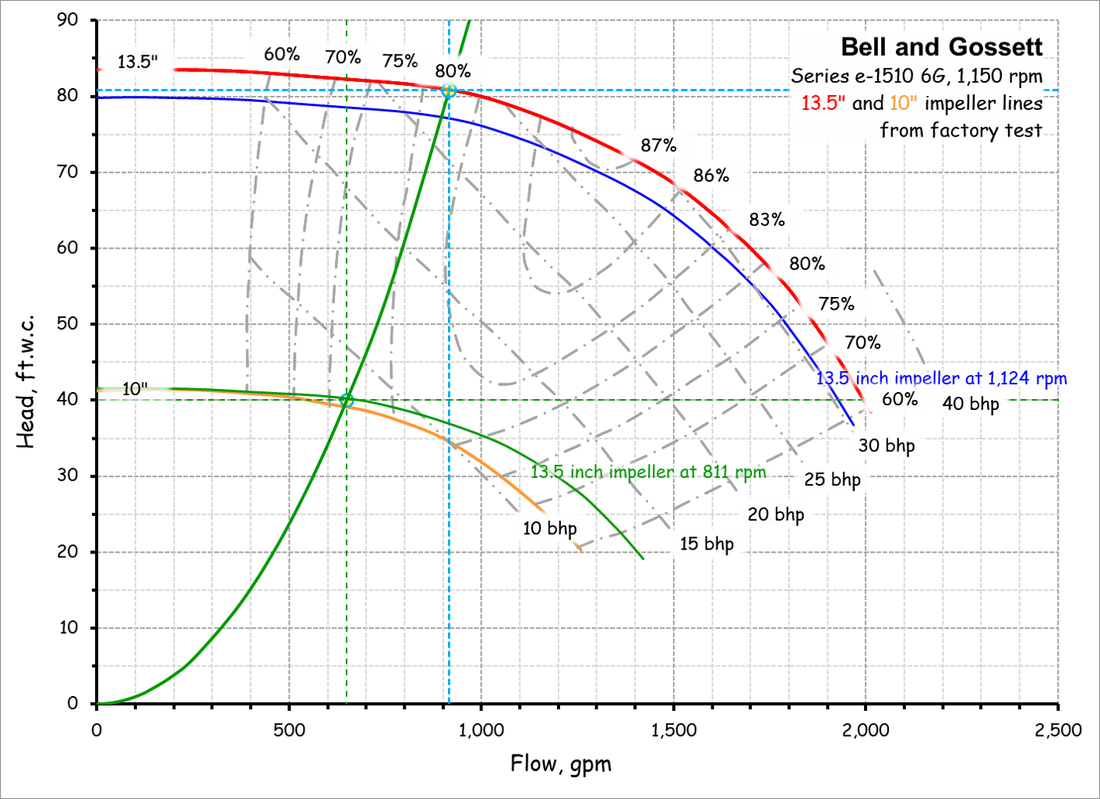
A Few General Affinity Law Concepts

This affinity law allows you to project the flow that will be produced with a larger or smaller impeller given a known operating point on a known impeller line.
Go There

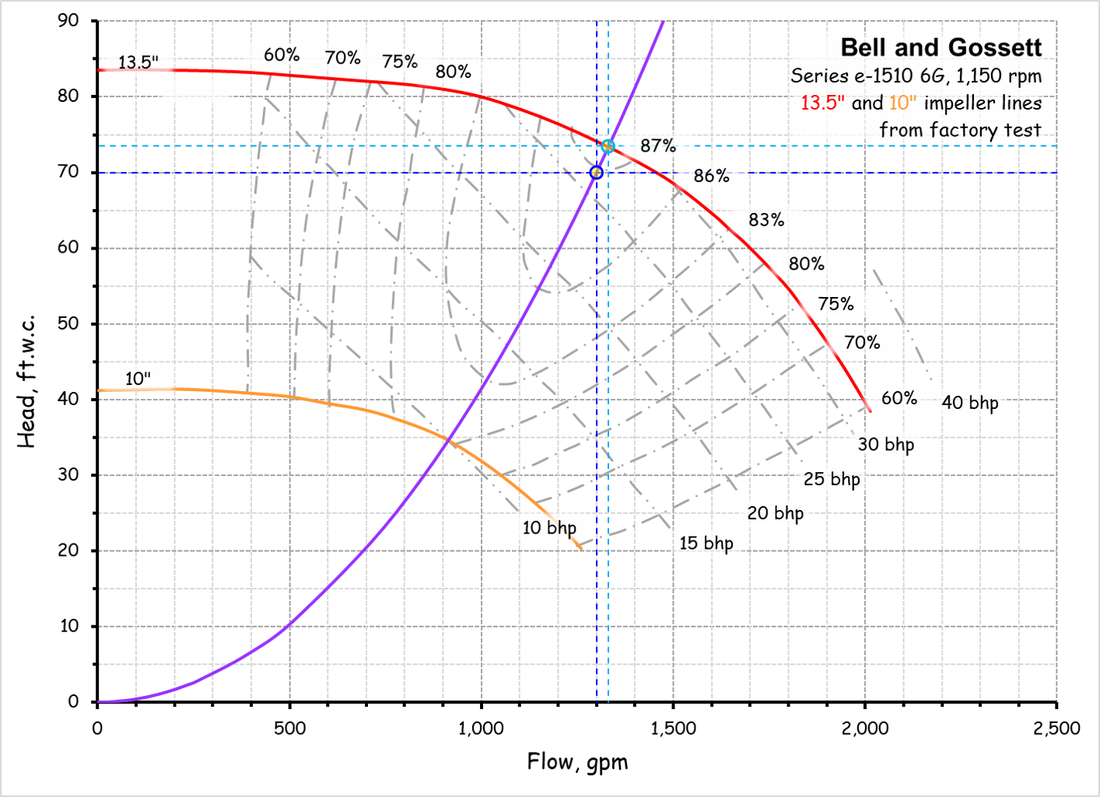
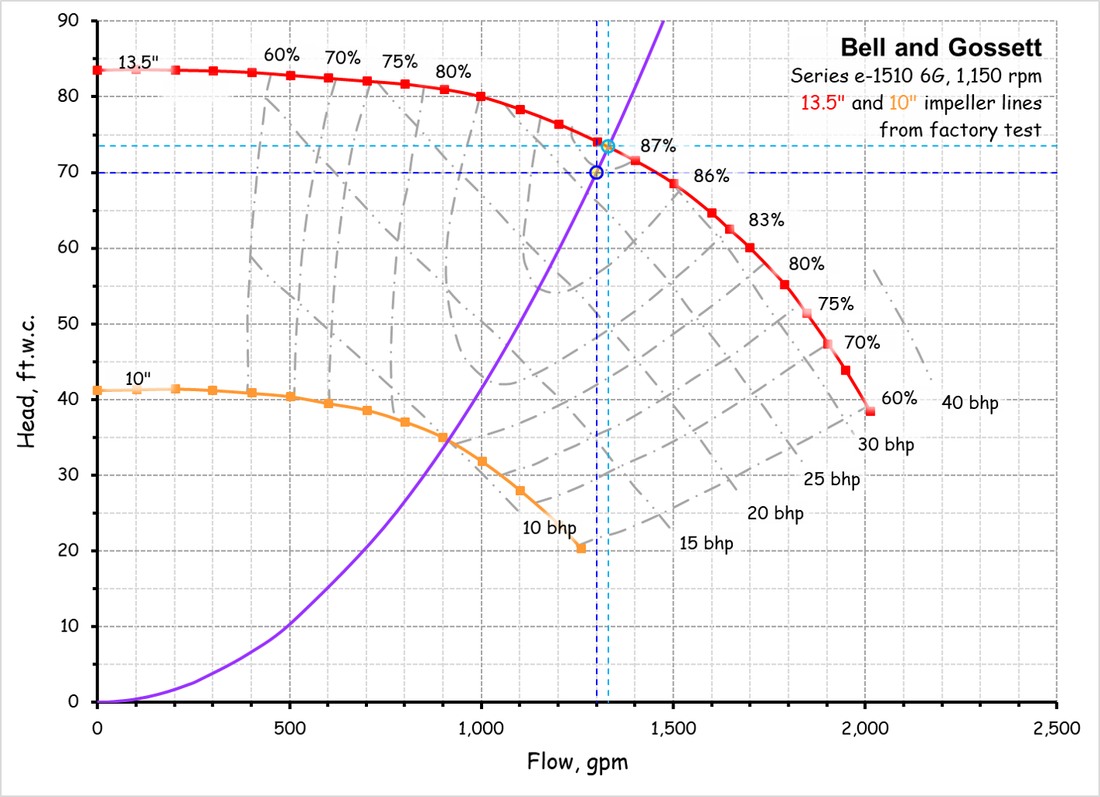
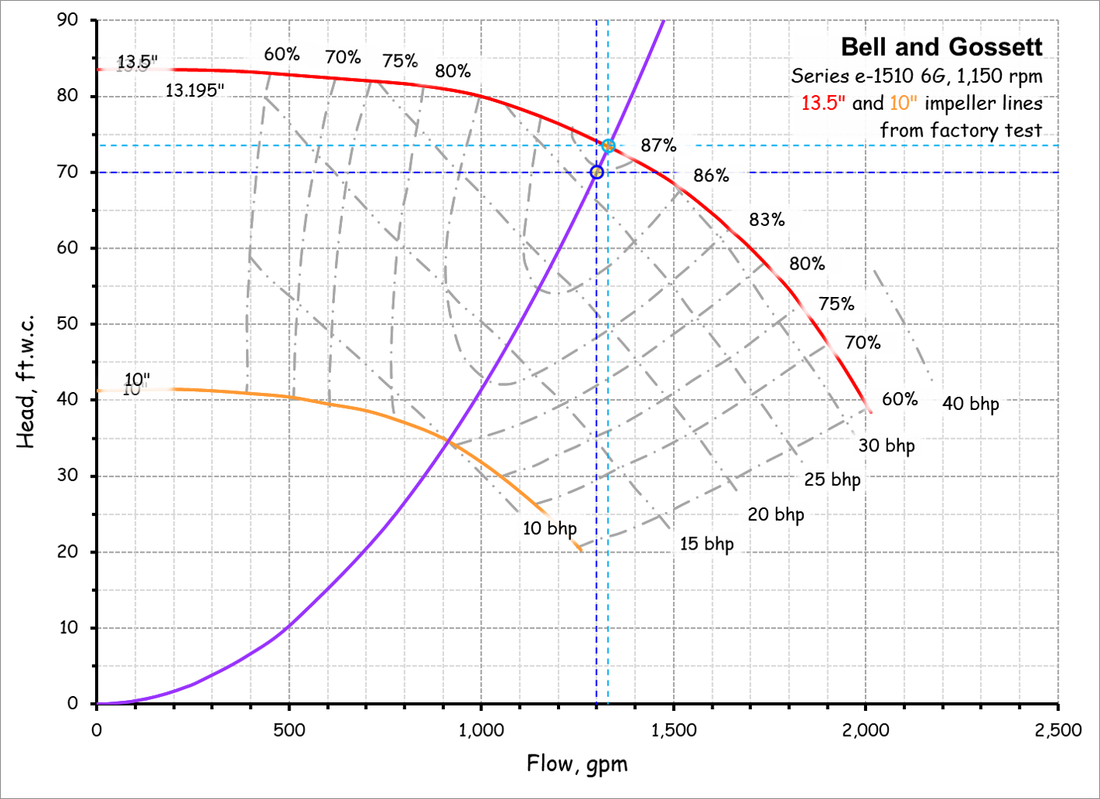
The Relationship Between Flow and Impeller Diameter

This affinity law allows you to project the flow that will be produced with a larger or smaller impeller given a known operating point on a known impeller line.
Go There

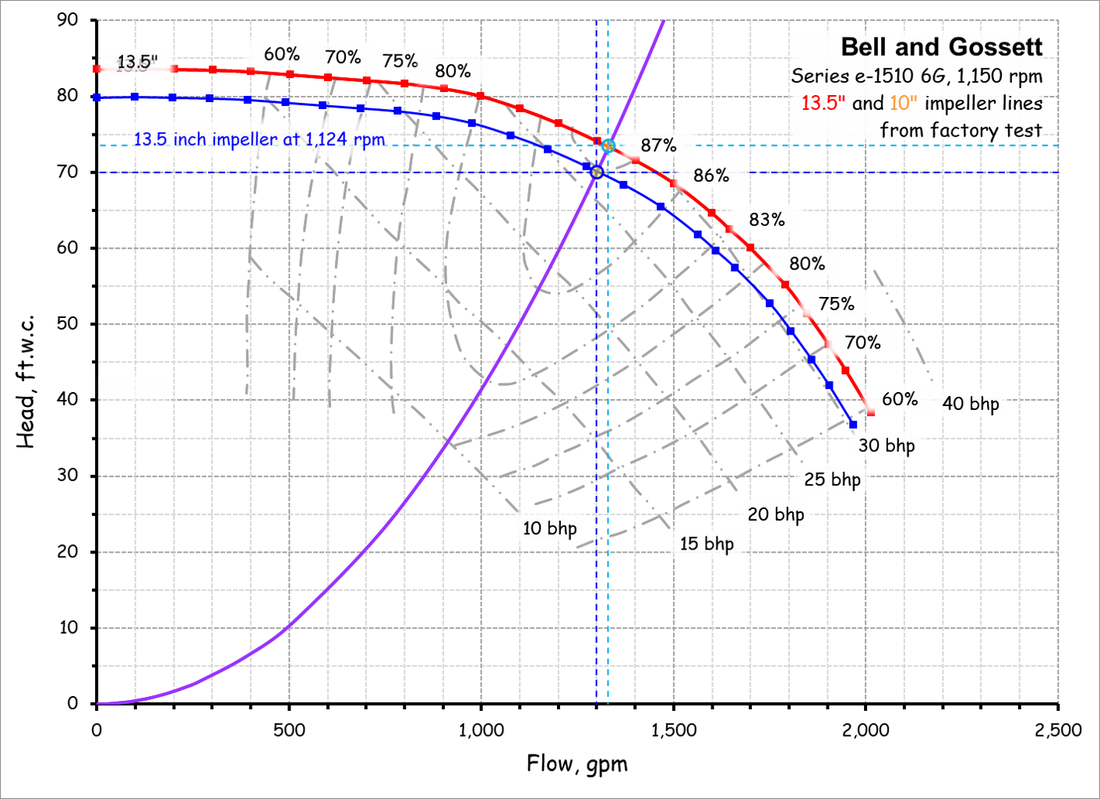
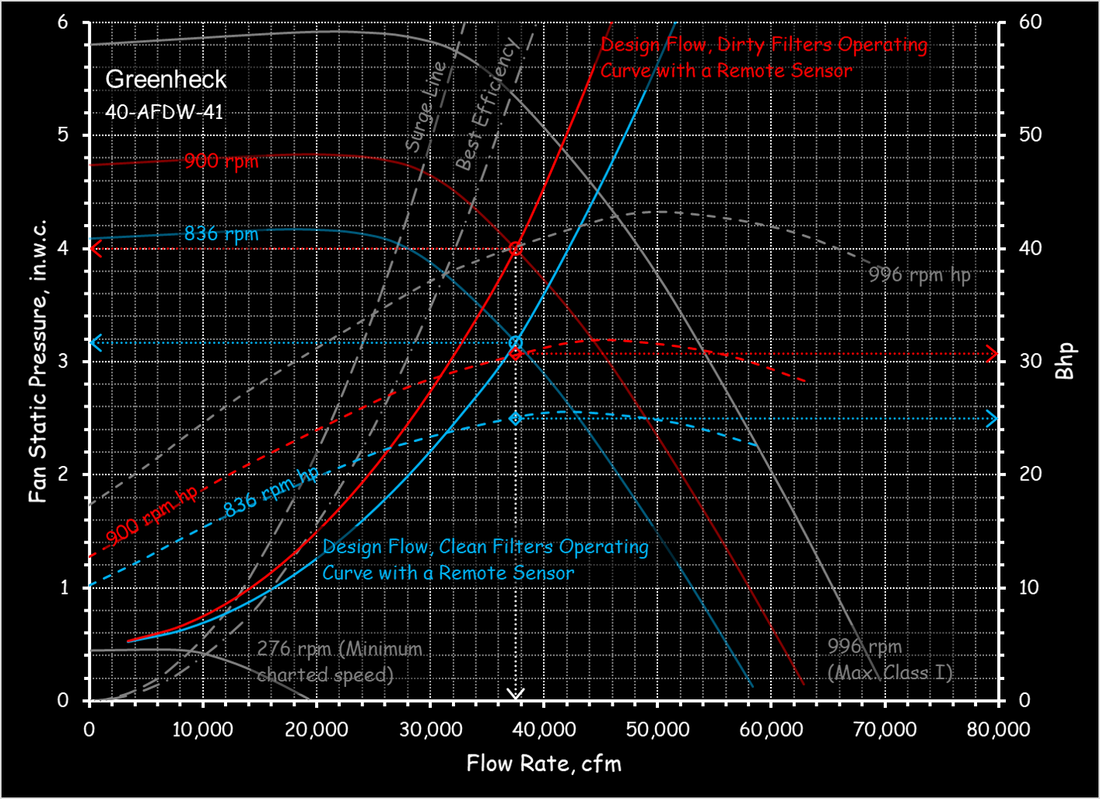
The Relationship Between Flow and Impeller Speed

This affinity law allows you to project the flow that will be produced with a given impellers size operating at different speeds given a known operating point on the impeller line.
Go There

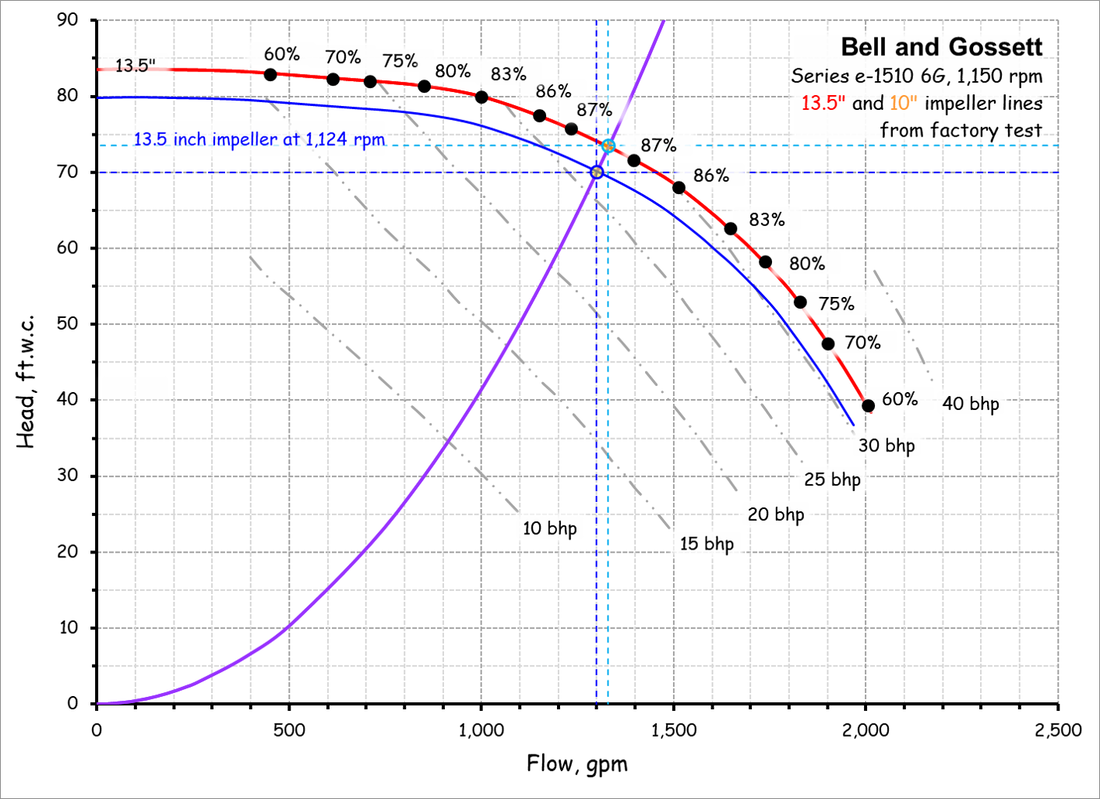
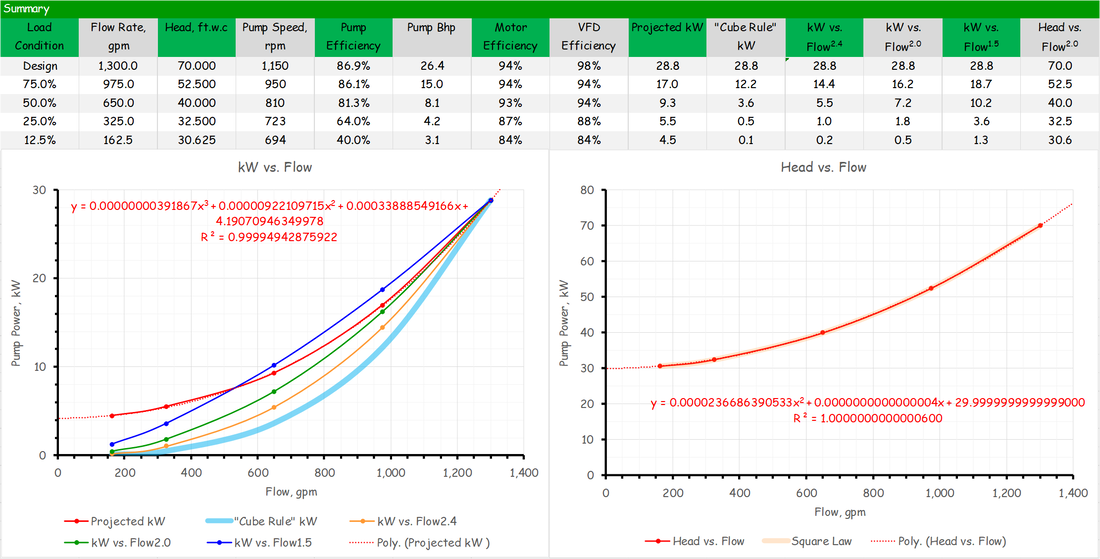
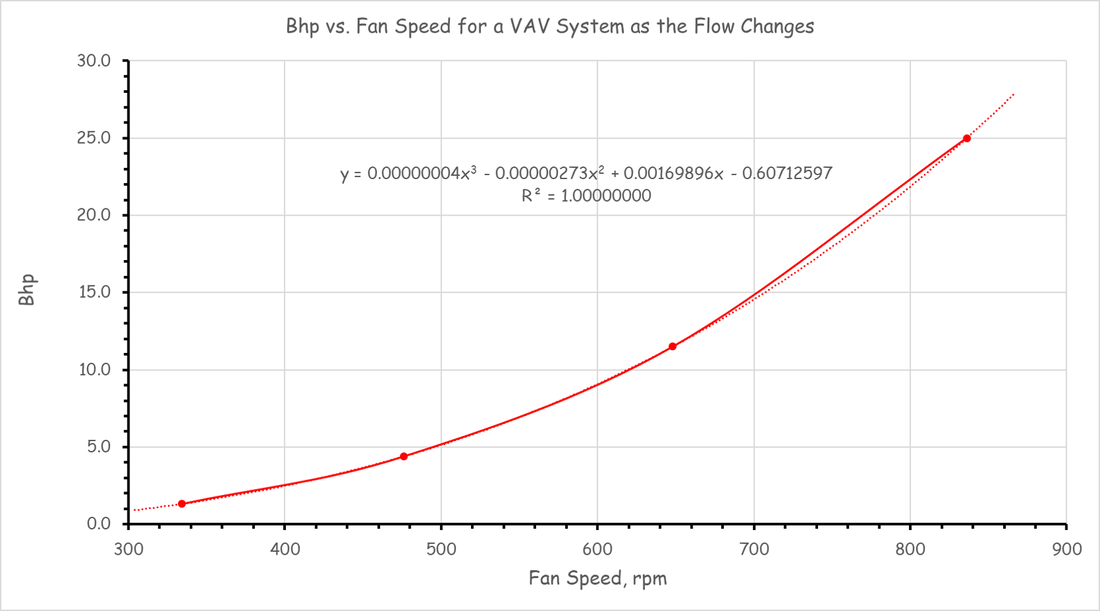
The Relationship Between Power and Impeller Speed; a.k.a "the Cube Rule"

This affinity law allows you to project the power required by a given impeller size operating at a given speed relative to what it requires operating at a known speed and operating point on the impeller line.  It is a cubic relationship and thus very powerful and attractive from an energy efficiency standpoint.  But it is also frequently misapplied.

In addition to the affinity law, this section illustrates two different techniques that can be used to project energy consumption based on a system's flow profile.
Go There

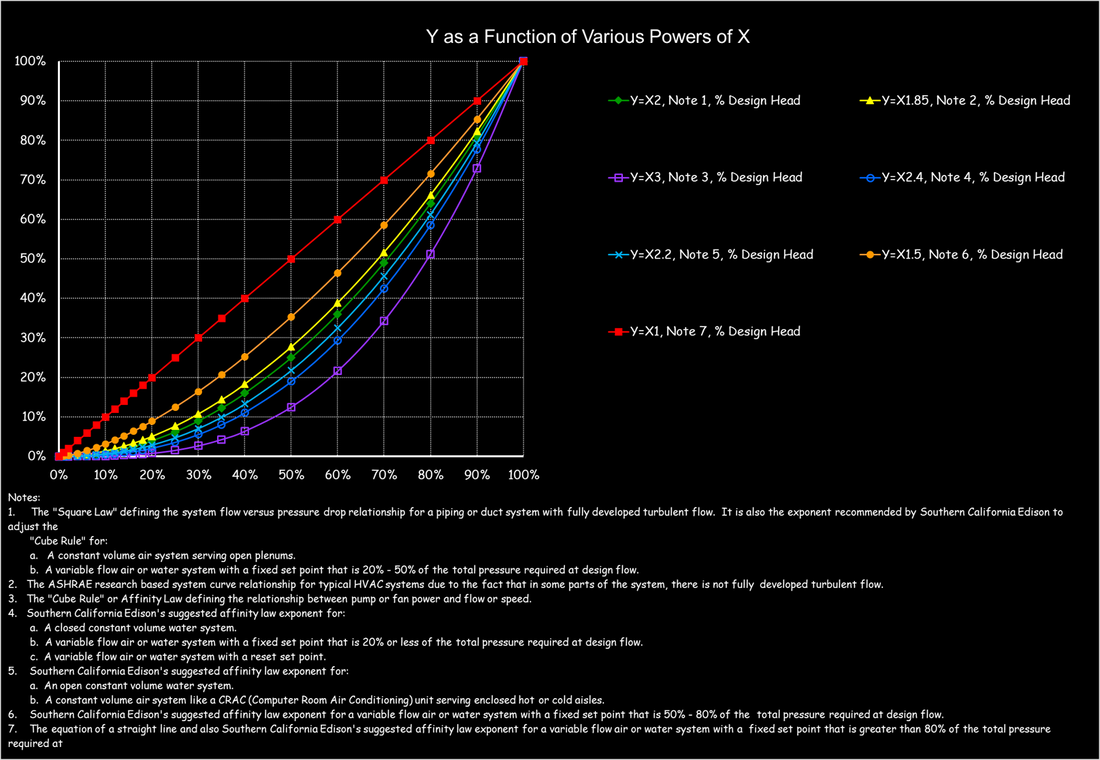
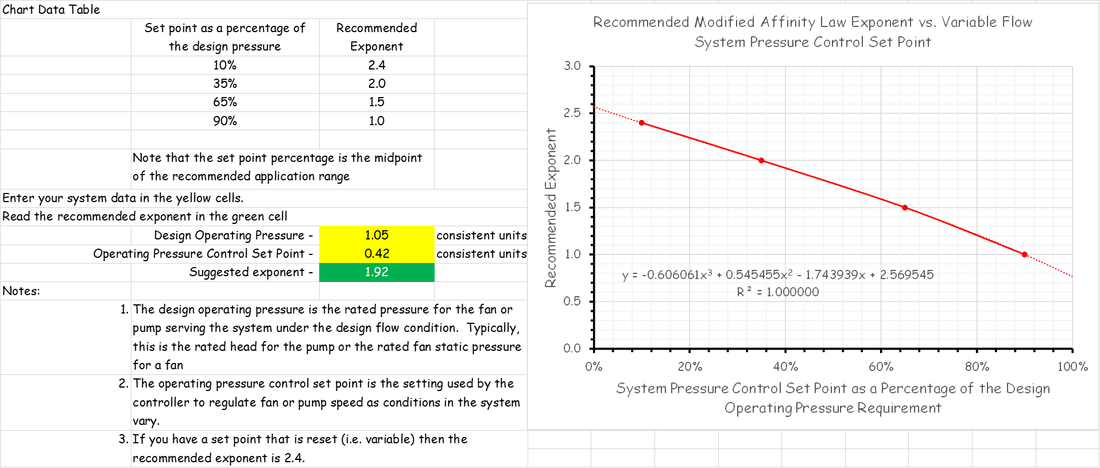
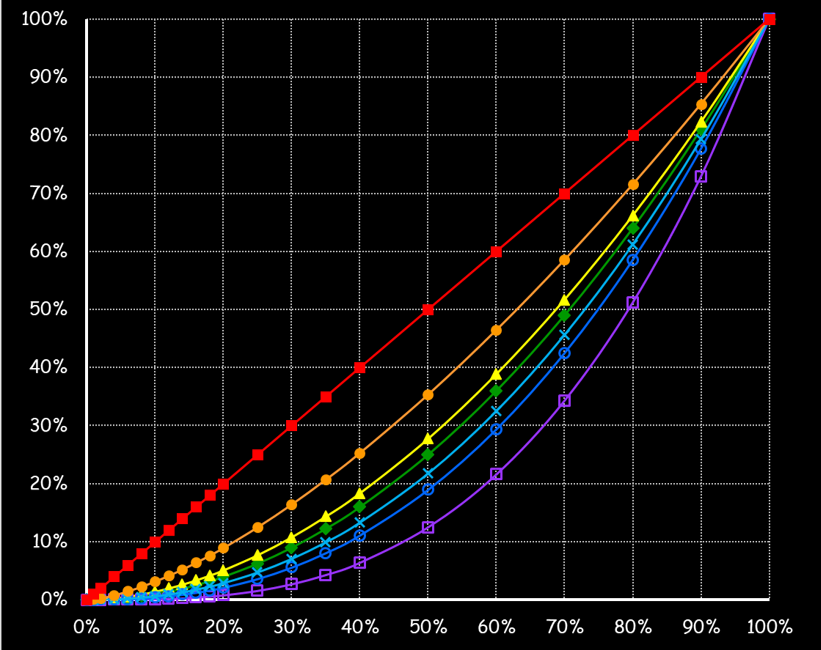
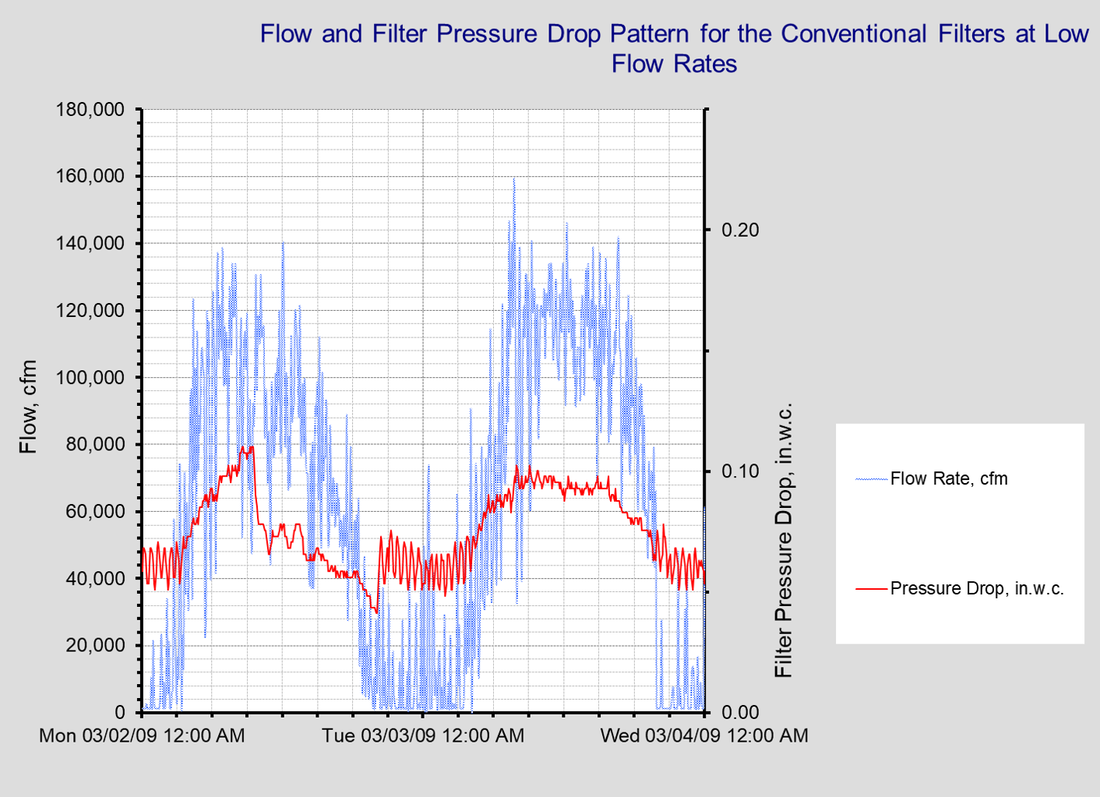
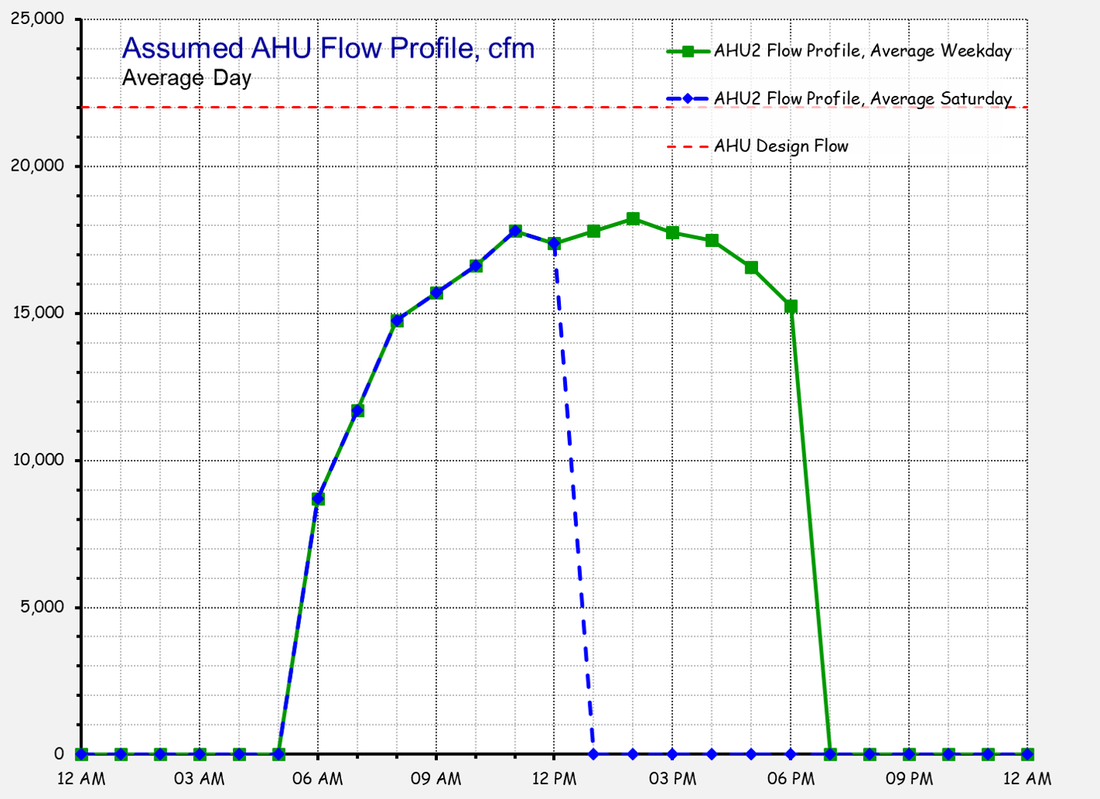
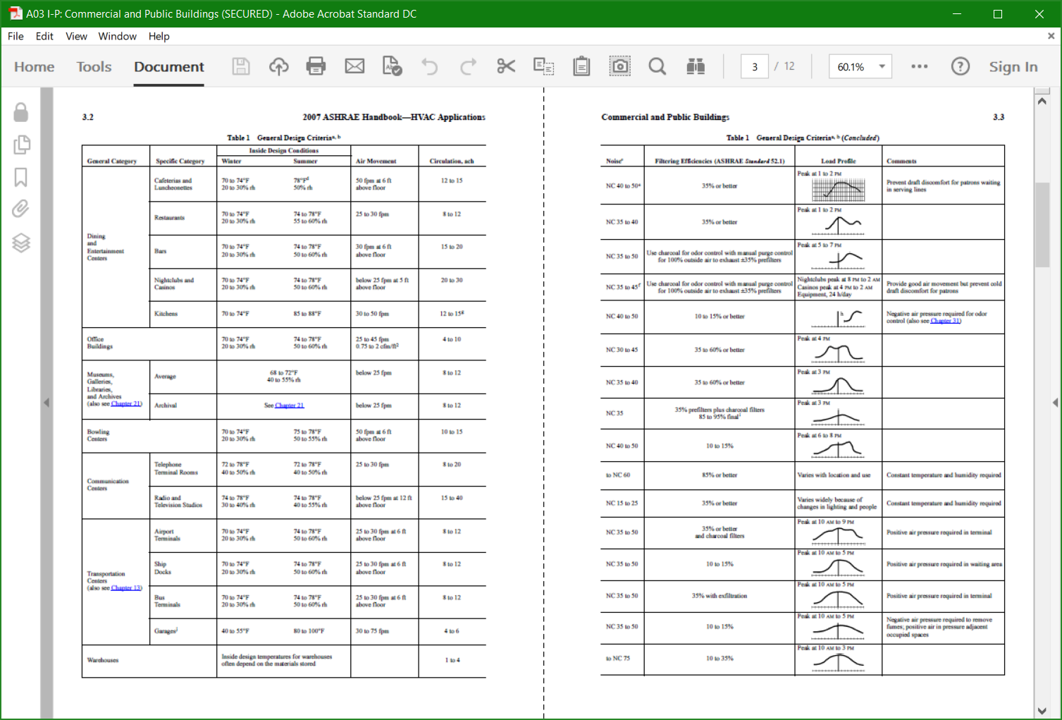
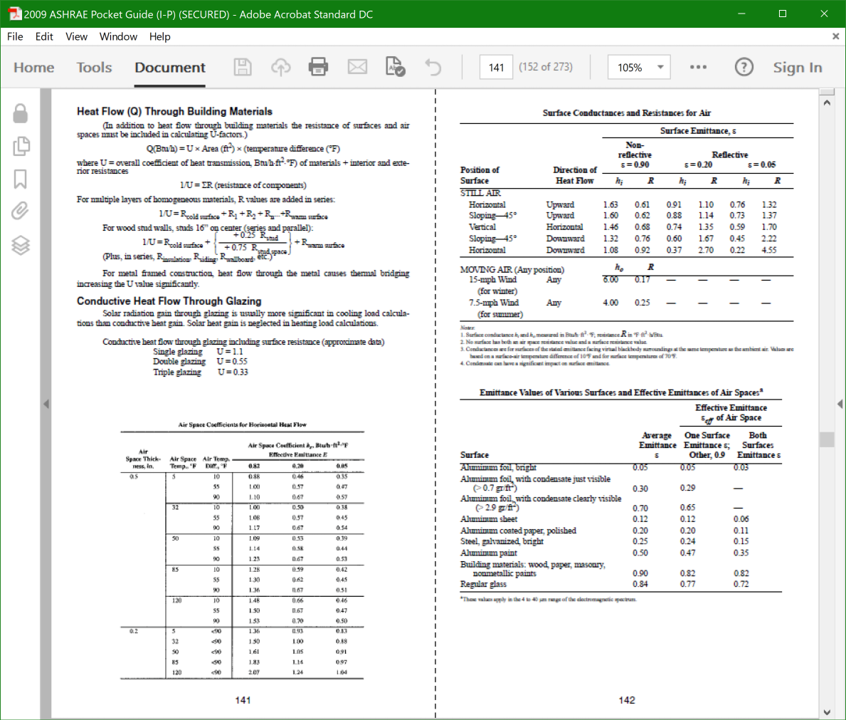
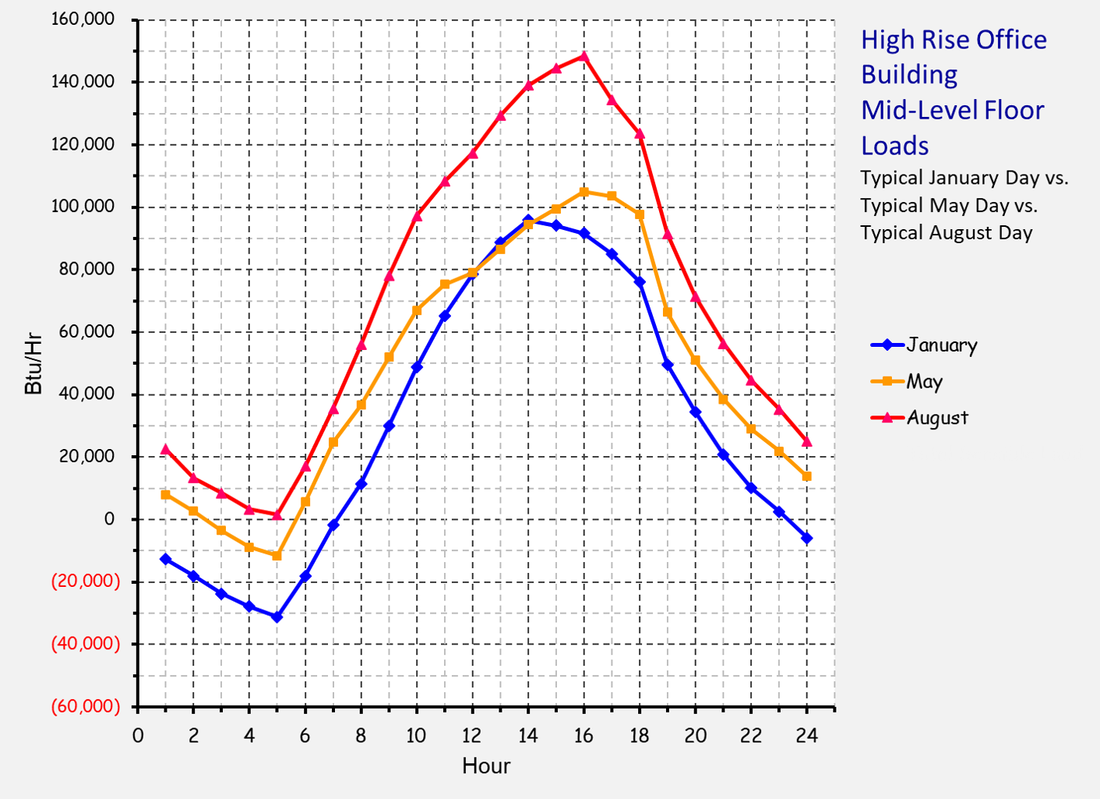
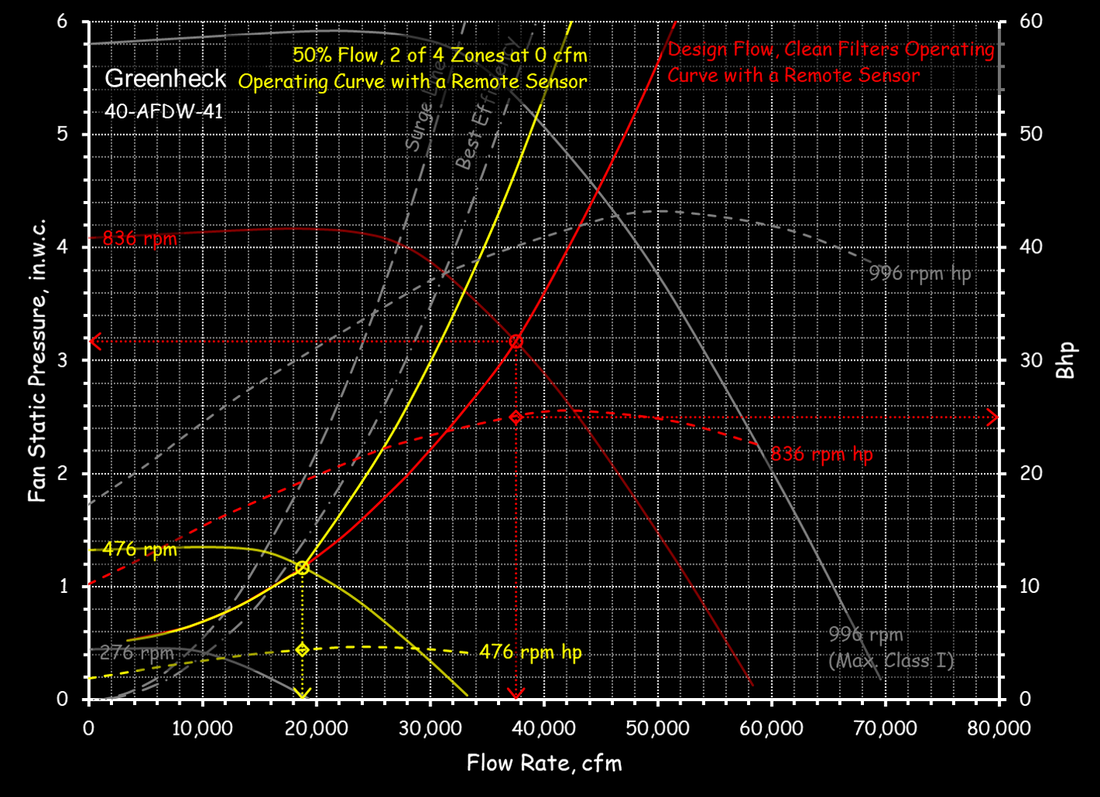
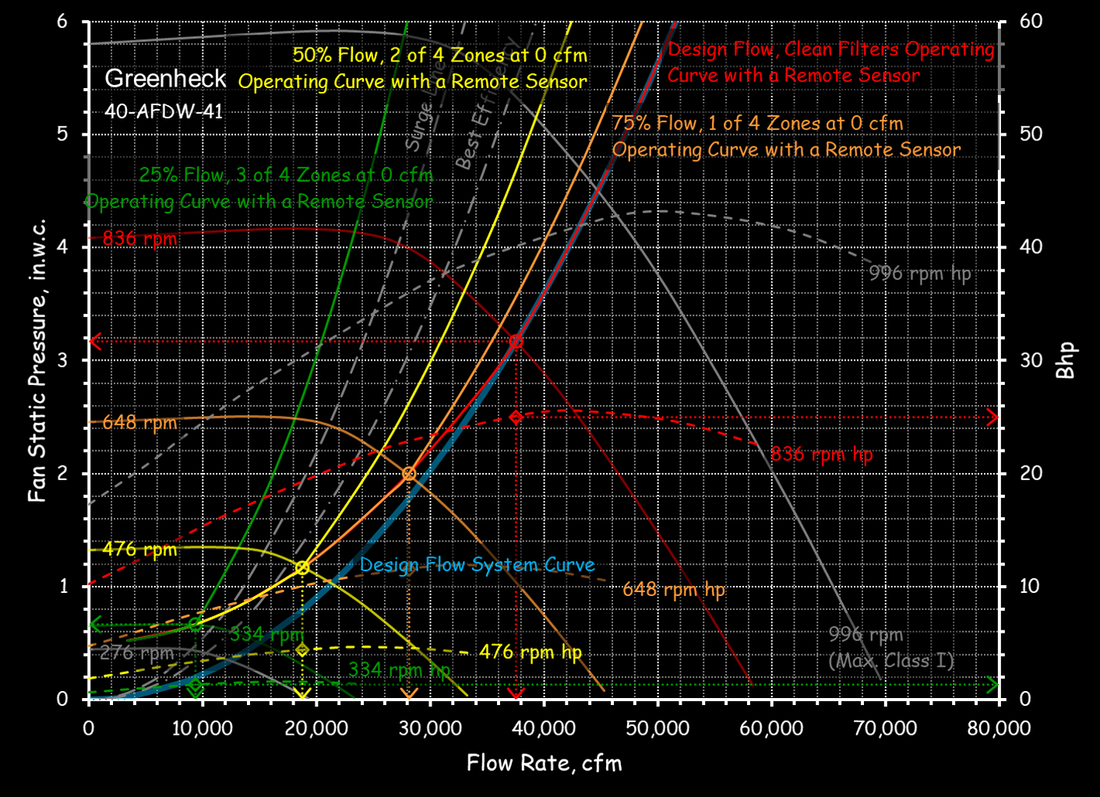
The Load Profile - A Key Element for Projecting Energy Use

As is discussed in the section about the cube rule, that law can be applied to project energy consumption for a fan or pumping system.  But variable flow systems introduce several complexities and one is the need to have a load profile to work from.   This section discusses some options for coming up with a load profile.
Go There

A Common Affinity Law Misapplication

Frequently, it is assumed that if there are two fans or pumps in parallel serving a load, the, via the cube rule, significant energy will be saved by operating both of the fans or pumps together at a lower speed as compared to operating a single fan or pump at a higher speed to serve the same load.

While this is true for some very specific cases (parallel independent cooling tower cells are a good example), it is generally not true.  This section discusses the reason and provides some resources to further explain the fallacy.
Go There


General Affinity Law Concepts
Affinity Laws Assume Geometric Similarity

There are a number of things to be aware of when you apply the affinity laws to predict the performance of a pump or fan.  One is that the laws are based on the concept of geometric similarity.   That means they assume that when, for instance, you trim (reduce) the diameter of the impeller in a pump, you change every other dimension of the pump proportionately;  i.e.;
  • The thickness of the impeller is decreased proportionately, and
  • The diameter of the volute is decreased proportionately, and
  • The diameter of the eye of the impeller is decreased proportionately, etc.
 The image to the left, below, illustrates this concept.
 What actually happens when we trim an impeller, is that the diameter of the impeller changes, but all of the other physical characteristics of the pump (or fan) remain as they were, which is illustrated in the right image above when you contrast the pump in it with the larger pump in the other image.

As a result, the actual performance curves associated with different impeller sizes will be different from what the affinity laws predict, as illustrated by the pump curve in the figure to the right above;  compare the solid lines (the lines predicted by the affinity laws from the red impeller line) to the dashed lines (the actual lines achieved based on testing by the manufacturer using the trimmed impellers.)
That doesn't mean you should not use the affinity laws to project a new impeller size.  It just means you should do it with the proverbial "grain of salt"; meaning you recognize the limitations.  For example, if you are projecting a new impeller diameter from an existing known diameter, your result will be much better if you project based on the closest known diameter.
For example, in the image to the left, the dashed red impeller line is the curve projected for a 10.5 inch impeller based on the known data for the 13.5 inch impeller (the solid red line).  In contrast, the orange dashed line is the curve for a 10.5 inch impeller projected from the known data for the 10 inch impeller (the orange line).

The solid green line is the actual test data based curve for the 10.5 inch impeller.  Note how much more closely the data projected from the 10 inch impeller matches the actual performance of the pump with a 10.5 inch impeller when compared to the data projected from the 13.5 inch impeller.

Affinity Laws Project Performance by Moving on a System Curve

Its important to realized that the affinity laws project points on a system curve through the point in question.   In other words, by definition, the design point we selected (the blue circle with yellow highlighting in the image to the left) is a point on a system curve that passes through it as illustrated by the purple line.

The system curve is defined by the "square law" and if you are not familiar with it, you can find out more about that on this page of the website.

The point where the system curve crosses the two known impeller lines (the red and orange 
lines in the image) is where the pump would operate if we installed it in the system we are considering with either the largest or smallest impeller in it.  In other words, with the largest impeller in it (the red line), the pump would move a bit more water and create a bit more head than we need to achieve the design target (the blue circle).  With the smallest impeller (the orange line) it would move much less water and generate much less head than we need.

We can use the speed affinity law discussed below to estimate the impeller size for our design point based on the known curves for the larger (or smaller) impeller.  We will get the best result by projecting from the largest impeller line since it is closer to the proposed operating point, as discussed above.


The Relationship Between Flow and Impeller Diameter
The Relationship

This affinity law allows you to project the flow that will be produced with a larger or smaller impeller given a known operating point on a known impeller line.   
Solved for Flow.wmf
File Size: 7 kb
File Type: wmf
Download File
Diameter Affinity Law.xlsx
File Size: 528 kb
File Type: xlsx
Download File
You can also use it to project the impeller diameter you will need to achieve a given flow rate given a known operating point on a known impeller line. ​
Solved for Diameter.wmf
File Size: 7 kb
File Type: wmf
Download File
In addition to simply projecting a new operating point, you can pick multiple points on the known impeller line and project the new impeller line associated with the new diameter.

Applying the Relationship to Generate A New Impeller Line for a Smaller Impeller

For instance, lets say we are considering the Bell and Gossett pump illustrated in the pump curve to the left for an application where we need to move 1,300 gpm at 70 ft.w.c. (the dark blue circle with yellow shading).   The curve has published data for its largest and smallest impeller sizes (13.5 inch and 10 inch), but our selection, while in a very efficient part of the curve, does not fall on one of the two published impeller lines.  Thus, we need to establish the impeller size required to achieve our design condition, which will be somewhere between the 10 inch and 13.5 inch impeller and closer to the 13.5 inch impeller size than not.
Since our operating point is a point on a system curve, we draw the system on the pump curve and project the operating point that the pump would achieve in our system if it had a 13.5 inch impeller. 
In other words, the point where the system curve intersects the 13.5 inch impeller line (1,330 gpm at 73.5 ft.w.c.) is where the pump we are considering would operate if we installed it in our system with the 13.5 inch impeller.  That gives us enough information to use the affinity law to project the impeller size, needed for the design condition as shown below.
This, of course assumes our calculated head requirement of 70 ft.w.c. is correct for the design flow rate of 1,300 gpm.

In the olden days, frequently, we would have simply sketched a curve in parallel with the 13.5 inch curve through our design point, labeled it 13.195 inches and called it good;  if we wanted the line to be particularly smooth, we might of used a french curve.  But if we wanted to be more precise, we would need to calculate a number of other points on the curve and then connect the dots to generate the new impeller line.

There-in lies the benefit of digitizing the pump curve and plotting it in Excel; you can quickly do the math to generate a new impeller line, system curves, parallel pump curves, etc. based on the digitized data.   

To plot the design point on the pump curve, we used two coordinates, the head, and the flow.  To plot other points on the new impeller line running through our design point, we will need similar pairs of coordinates.   
 When you use Plot Digitizer to pick up lines from an image so you can load them into Excel and plot them, you are actually creating a string of points that you then plot as a line in an Excel chart.  In the image to the left, I turned on the point markers (the red and orange dots) for the two impeller lines that I digitized so you could see this.

That means that to create my new impeller line, I simply need to set up a table that is built from the Plot Digitizer data for one of the impeller lines.  Ideally you should use the known line closest in size that you are trying to project, which in this case is the 13.5 inch impeller line.
The image to the left is an example of this type of table.  Specifically, Columns A and C are the digitized data points created using Plot Digitizer.   (In the olden days, these values would simply be arbitrarily selected points that we manually read off the pump curve.)

Column B is calculated using the affinity law relating flow and impeller diameter.
Column C is calculated using the square law based on the values in the other columns.
The image to the left illustrates this on the pump curve for the one (green) point.   The new impeller line is defined repeating the same calculation for the other red dots to project additional points (the blue dots) on the line.
Connecting the dots creates the new, impeller line associated with the impeller size that will deliver the design flow and head (the blue circle with yellow shading).

The Relationship Between Flow and Impeller Speed
The Relationship

This affinity law allows you to project the flow that will be produced for different speeds given a fixed impeller size and a known operating point.   You can also solve it for speed to predict the speed required for a given impeller to produce a targeted flow rate on a fixed system curve. 
Solved for Flow and Speed.wmf
File Size: 10 kb
File Type: wmf
Download File
Speed Affinity Law.xlsx
File Size: 536 kb
File Type: xlsx
Download File

Applying the Relationship to Generate a New Impeller Line for a Different Speed

As was the case for the diameter affinity law we discussed above, you can also do the calculation for multiple points on the known impeller line to construct the impeller line at different speeds.  The techniques you would use to do that are identical to what is illustrated above, so I will not go through that again.

But, to illustrate applying the law, lets project the speed we would need to achieve the design operating point of 1,300 gpm at 70 ft.w.c. that we used in the example above so we can compare trimming the impeller with using a variable speed drive of some sort to achieve the same result.
The starting point is the same for both procedures; i.e. project the system curve through the design point to find out what flow would be produced by the full sized impeller at full speed if it was installed in the system in question.  In this case, that turns out to be 1,330 gpm at 73.5 ft.w.c.

Now you just do the math.
Knowing the speed you need, you can then solve the equation for flow and use the new speed and the reference speed for the pump curve (1,150 rpm in this case) to come up with the flow associated with points on the new impeller line based on flow points on the known impeller line (the red dots on the red line).
Finally, use the square law to calculate the head associated with each flow point using the flow and head from the known impeller line along with the flow at the reduced speed and connect the (blue or color of your choice) dots.
The blue impeller line associated with 1,124 rpm is basically the same line as the blue impeller line associated with the smaller impeller that we generated above but with a couple of important differences.   

For one thing, changing the speed did not change the geometric relationship between the pump impeller and volute.  So geometric similarity is preserved and the slight change in curve shape associated with an impeller trim associated with a lack of geometric similarity before and after the trim are eliminated.

For another, changing the speed of the impeller tends to preserve the efficiency of the impeller because the things that impact pump efficiency are not much affected by speed.  In fact, lowering speed tends to produce a modest increase in efficiency because, for instance the bearing losses are lower since the pump is spinning slower.

In this example, the impeller trim shifted the impeller efficiency a bit;  from a bit above 87% to slightly under 87%, so maybe a 1% or so loss at the most.  Of course a bigger trim would have changed the efficiency more since you would move further down the system curve.
In contrast, slowing the impeller down with a variable speed drive preserved the efficiency at the point where the system curve crosses the 11.5 inch impeller line when it is running at full speed.  So in a way, the efficiency lines on the pump curve for speeds below the full speed for the impeller are meaningless. 

​In fact a more accurate way to represent the pump curve for variable speed operation might be to turn off the efficiency lines and just plot the points where they cross the impeller line, something like the image to the left.
So at first blush, the variable speed drive would seem like the better efficiency option.  But, variable speed drives are not 100% efficient.   For example, Variable Frequency Drives (VFD's), which are the most common variable speed technology currently, have a 2-3% efficiency loss or more at full speed and they become less efficient as the load drops from full load. 

So, if we only needed to shift the operating point of the pump one time for balancing purposes, for this particular example, the impeller trim would be a more efficient option because of the losses imposed by the variable frequency drive.  But, if there was a need to constantly change the pump speed because it was serving a variable flow system, then a variable speed drive is kind of God's gift to HVAC and would be the way to go.   If you want to look at a pump optimization example that compares all of the options, including a VFD, an impeller trim, and a right sized pump as a solution, then you might find this slide deck to be of interest.

For more on variable speed drive efficiency, the string of blog posts that start with this one explore VFD efficiency a bit.   This post includes a section that looks at hydraulic variable speed drives and include a reference that contrasts their efficiency with VFD efficiency.
If you needed to shift the operating point more significantly relative to what you would get with a full sized impeller, the efficiency penalty associated with an impeller trip becomes much more significant, as illustrated in the pump curve to the left. 

More specifically, if we needed to achieve 650 gpm at 40 ft.w.c., then we would need to either drop the pump speed to 811 rpm, which would preserve the pump efficiency at about 81.5% but cost some losses in the drive. In contrast, if we trimmed the impeller, the pump efficiency would end up at about at about 76%. with an impeller size that was slightly larger than the smallest possible 10 inch impeller.
The other detail to notice is that if we slowed the pump down, in addition to preserving the pump efficiency, we will also preserve the curve shape.  Trimming the impeller will cause the curve shape to change due to the geometric similarity considerations discussed previously (compare the green impeller line with the orange impeller line).
One final point;  if you open up the Speed Affinity Law spreadsheet, you will notice that I have a cell that allows me to "tweak" the pump speed.   The reason for that is that because things like rounding errors, the accuracy of test data, etc. can cause the projected impeller speed line to not pass exactly through the point you are considering, especially for a large speed change.  So to get things visually correct, I included a cell that lets me shift the projected curve slightly so that everything looks right.   
The reality is that the affinity law projections will get you in the ball park.  In the field you may need to fine tune them;  in the case of a speed projection, you may end up increasing or decreasing a few rpm from the projection to get what you want (unless the control system automatically does it for you).  For an impeller trim, its best to err on the high side (trim the impeller a little large) and then throttle to fine tune things if you need to.


​The Relationship Between Power and Impeller Speed
The Relationship

From an energy conservation stand point, this affinity law is really exciting (in a nerdy sort of way) because it basically says that if you cut the flow in a pipe or duct system by 50%, the fan or pump will only use 12.5% of the power required at full flow.   But this only applies to  a fixed system;  more on that in a bit.  This law is often referred to as "the cube rule" and since speed and flow are directly related, you can also say that power will vary as the cube of the speed of a pump or fan.
Bhp and Flow.wmf
File Size: 12 kb
File Type: wmf
Download File
​For example, consider two identical cooling tower cells where, as the load increase, water flow is directed over the first cell and its fan is staged on and ramped up to full speed.  If the load continues to increase, water is also allowed to flow over the second cell and its fan  is staged on and ramped up to full speed.  In this scenario, when the system served is at 50% load, one cooling tower cell will have water flowing over it and its fan will be at full speed.  The other cell will have no water flow and its fan will be off.

It would also be possible to allow water to flow over both cooling tower cells at 50% load (assuming you could get good water flow distribution over the fill in both towers at 50% design water flow per cell) and ramp both fans up together.   As a result, at 50% load, each fan would be at 50% speed.  Because most cooling tower cells are fixed systems, the cube rule can be applied and the power used in this operating mode is only 12.5% of the maximum per fan or 25% (12.5 % times 2 fans) of the power that was being used running one fan at full speed to serve the same load condition.

In basic terms, a fixed system is one where nothing in the air or water flow path moves under any operating condition.   Most cooling towers meet this criteria since there are no dampers in the air stream and the fill is uniformly wet.  Thus, the system curve for the air flow path through the tower is constant.

In contrast, most variable flow/variable speed systems operate over a range of system curves. For example, in a variable flow pumping system, the steepest, low flow system curve is likely the one created under a minimum load condition where all of the two way valves at the loads have fully closed and the only flow that exists is due to a few three way valves provided for the purpose or via a minimum flow bypass.  The shallowest, highest flow system curve is likely created by a condition where all of the valves in the system are wide open.

In a variable flow air handling system, the steepest/low flow system curve is likely the curve created with all of the terminal units at minimum flow.  The shallowest, highest flow system curve is likely created by a condition that drive all of the terminal units to maximum flow, perhaps starting up with a hot building.

Applying the Relationship to Project Energy Savings Using SCE's Affinity Law Coefficients

In an effort to provide some method to assess energy consumption and savings opportunities for variable flow systems, Southern California Edison (SCE) in conjunction with several other California public utilities did some modeling and developed a set of recommended exponents that could be applied to the affinity laws to predict the energy consumption and savings that would be achieved by making improvements to variable flow systems.  The image below is a plot of the various exponents they came up with along with what the bhp vs. flow affinity law would predict.
The spreadsheet below contains the graph shown above along with a tool that interpolates between the different SCE coefficients to allow you to pick one that is a good fit for your application.   The .pdf file is the original SCE publication with the coefficients in it.
SCE Coefficients Tool.xlsx
File Size: 176 kb
File Type: xlsx
Download File
SCE 2013 Variable Flow Affinity Law Recommendations
File Size: 118 kb
File Type: pdf
Download File
The concept behind the SCE coefficients (at least how I think about it) is that while the family of system curves associated with variable flow systems make it improper to say that power will vary as the cube of the flow, real systems will approach that relationship and could be modeled by using some other exponent less than three.   The value selected for the exponent is related to how well the control process used to control pump or fan speed is optimized in terms of only producing the amount of pressure required by the current load condition, no more, and no less.​
Consider the air handling system illustrated to the left where I have removed the floor, walls and ceiling above the mechanical room so you can see the entire supply duct system.  (FYI, this is the Ball Room AHU Scoping exercise model if you want to actually look at it more closely or from different angles).

For our discussion, assume the system is a two zone VAV reheat system and that the tee in the supply duct towards the top center of the picture is where it splits to serve each zone.
We will also assume that to deliver design flow, we need to maintain 1.05 in.w.c. in the supply duct at the discharge of the fan, which creates a pressure, at design flow, of 0.42 in.w.c. immediately ahead of the tee where the duct splits to serve the zones.
If I control the supply fan speed based on the pressure at the discharge of the AHU, then no matter what the load condition is, I will always need to generate 1.05 in.w.c. of pressure to guarantee that I deliver flow as needed at the zone level.   I will still save energy as the flow varies since fan power is a direct function of both flow and static pressure, as illustrated in the equation to the left. 
​But at reduced flow conditions, with lower pressure drops in the duct, the fan will make more static than is actually needed to overcome the pressure drop between the discharge and the tee,  which will end up being dissipated by the terminal units closing their dampers more than they would need to if I reduced the discharge static pressure as the load dropped off.

One way to address this is to use a reset schedule that lowers the discharge static pressure based on some indication of load.  Another way to do it is to leverage the two thirds rule and locate the sensor out in the distribution system. 

For example, if we located the sensor for the AHU in the illustration immediately before the tee and controlled for 0.42 in.w.c. at that location (which is what it takes to deliver design flow to either of the zones), then, if both zones were demanding full flow, the sensor would speed the fan up to deliver the required 1.05 in.w.c. at the fan discharge because it takes that much pressure to overcome system effect and the pressure drop in the duct system and deliver 0.42 in.w.c. ahead of the tee.
 But, for example, if one zone was fully occupied while the other zone was totally unoccupied, the system could use a zone level scheduling strategy and forced the damper serving the unoccupied zone closed, which would reduce the flow requirement by 50%.   As a result, the pressure drop due to flow in the duct system between the fan discharge and the tee in the duct system would only be 25% of what it was at design flow, as predicted by the square law and illustrated to the left.

In some ways, the remote sensor "sees" the pressure drop due to flow between the fan discharge and its location.  In this case that means that a remote sensor controlling  fan speed
would reduce the pressure at the fan discharge to approximately .58 in.w.c. at a 50% load condition.

If you study the SCE recommendations, you will realize that they say that you can increase the exponent you use (i.e. project more energy savings) as the set point you control the system for is reduced relative to the design pressure.  
For our example the remote set point is 40% of the design static requirement, so if you interpolate the SCE coefficients using the ​spreadsheet tool above, then you would use an exponent  of 1.92 to project the energy consumption of the 
system as a function of flow for the system using the sensor at a remote location (see the screen shot below).
If you were proposing relocating the sensor from the fan discharge to the remote location as an energy conservation ​strategy, ​
then you could estimate the savings by using an exponent of about .77 to estimate the "as found" energy consumption.
Finally, if you subtracted the energy consumption projected using the 1.92 exponent (representing what would be achieved with a remote sensor) from what was projected using the exponent of .77 applied to the same flow profile, you would have identified the savings that would be achieved when the strategy was implemented. 

Having said that, if you decide to move a sensor from the fan or pump discharge to a remote point in the system, there are are several important issues you need to consider.
  1. Moving the sensor to a remote point will introduce lags into the control process, primarily due to the transportation delays but also due to the dynamics of the distribution system, especially for air systems.   Lags can make a control process difficult or impossible to tune and can lead to things like blown up duct, which is how I discovered this.
  2. From an installation cost standpoint, it is tempting to wire the remote sensor to a nearby controller and then transmit the data over the network to the controller that is managing the variable speed drive instead of running a cable all of the way to the location.  It is bad practice to make a control network an element inside a control process like a PI or PID loop because it can introduce another lag that will vary with the network traffic rate, making the turning even more difficult and because it sets up the process to go open loop (out of control) if there is a network failure.
  3. On large distribution systems, identifying the critical branch - i.e. the branch with the worst case pressure drop (which is where you want to put the sensor) - can be challenging because of the complexity of a large distribution system and its dynamics.
Item 1 and 2 can be dealt with by using a cascaded control strategy.  In other words, the control process runs locally at the variable speed drive controller location based on the discharge pressure from the fan or the pump.   The data from the remote sensor is used to adjust the set point of the control process, rather than as its input, which allows it to optimize the process based on the remote condition and also allows the information to be sent to the primary controller via the network since it is adjusting the control process rather than the input to the control process.
​
Item 3 can be addressed by using several remote sensors and then averaging them or picking the lowest signal as the one that will be used to optimize the primary control process.
Lags and the Two Thirds Rule.pdf
File Size: 4997 kb
File Type: pdf
Download File
The presentation to the left will provide some additional insight into the two thirds rule and the adverse impact lags can have on a control process (including my little blown up duct adventure) along with ways to deal with lags.

Developing Your Own Power vs. Flow Relationship from the System Characteristics

One of the things that is bothersome about an approach that uses the SCE coefficients (or even the cube law) is that it predicts that the power required will go to zero when the flow goes to zero.   While that is true in terms of the energy represented by the mass in motion in the duct or pipe, I think we could all agree that if the fan or pump and its motor are spinning, then the system will be using energy due to efficiency losses in the motor, drive system and fan wheel or pump impeller, even if it is not moving air or water to the load.

That implies that if you simply used the coefficients, they would tend to over-estimate the savings at part load hours.  Of course, once you recognize the problem, you can address it by manually limiting the minimum power to some value you
come up with via a test or an analysis of efficiency losses or some other means.   But it occurred to me at one point that you might be able to develop your own relationship for power as a function of flow based on an analysis of the system using the pump or fan curve associated with it along with information about how motor and drive efficiency varied with load.   
Flow vs. Power from a Curve Analysis.pdf
File Size: 2669 kb
File Type: pdf
Download File
Currently, time precludes me from going into the details of that.  But the presentation to the left illustrates the technique and the results compared to the SCE coefficients are illustrated below.
Note how the relationship that was developed with the technique (the red line) represents a more real model of what the power would actually do as the flow dropped off (i.e. never go to zero) as compared to the SCE curves and the cube rule (the other lines).  

Using the SCE coefficients will, of course, be a faster way to go.  But what I like about the technique, aside from its addressing the power consumption at part load more realistically (in my opinion), is that because it is based on the the pump (or fan) curve and other data for the system, it is pretty specific to the system vs. the more generic nature of the SCE coefficients.   So I offer it for what it is worth.

If you decide to try it here are a few things to consider.
  1. It will take more time than using the SCE coefficient approach.  But once you have the spreadsheets set up and have learned the technique, repeating the process will be much easier.
  2. It is only as good as your estimate of the pressure drop in the system between the pump or fan and the remote sensor location. 
  3. In the example, I clustered all of the loads at one end of the pipe and made an assumption about a low pressure drop header connecting them all together, which simplified the analysis over what would be required if the loads were distributed along the mains at various points.
  4. Having a digitized pump curve like one you might create using Plot Digitizer makes this a much more viable technique than doing it manually by plotting lines on pump or fan curves.


The Load Profile - A Key Element for Projecting Energy Use

 One of the biggest challenges associated with doing fan or pump energy calculations on variable flow systems is coming up with the load profile, which typically, is what drives the flow profile.  The load profile can vary with the season, time of day and day of week. 

Back in the olden days, when a spreadsheet was one (or more) pieces of graph paper that we drew a table on and then used slide rulers and calculators to come up with numbers to put in the squares in the table, performing an hour by hour calculation was impractical. So we used bin data to simplify the process to one where we only needed analyze 20-30 different conditions instead of 8,760 conditions (the number of hours in a year).

But with computers, going the hour by hour route adds accuracy and flexibility.  And the reality is once you figure out the math for one condition (i.e. one row) of the spreadsheet, most of the time, you can calculate the other rows by simply copying and pasting your math to them.  So assessing 25 bins or 8.760 hours is not that much different;  you spend all of the time on that first row getting the math right.

If you want to compare what might have happened in the past if you had done something differently, then you probably want hourly weather data for the particular point of time that is of interest.   This blog post and the ones that it links to will fill you in on a number of ways to come up with historical hourly weather data and how to work with it.  Currently, my go to place for hourly weather data is the Iowa State University website you will find at this link;  it really makes it easy.   You will also find a number of resources for climate data in the blog posts at this link.

If you are wanting to project what will happen in the future, then you probably want to use a normalized weather data set for a particular site vs. an actual hourly weather data set because the actual data will have extreme conditions (or not) that could cause you to overstate (or understate) the average savings you will achieve.   Data files like this are called TMY files for Typical Meteorological Year and can be downloaded in a raw form from NREL.   

If you go that route, you will probably want to install kW Engineering's Get Psyched plug-in so that you have function calls like Enthalpy, WetBulb, etc. built right into Excel.  It's free and a wonderful resource for the industry and you can download it at this link.

Another option is to use the climate data files that are part of the package you get when you buy an electronic psych chart.   This link takes you to a blog post that shows you how to use a free electronic psych chart that Ryan Stroupe of the Pacific Energy Center has made available.  Ryan also worked out a deal with the vendor that allows you to upgrade the chart to the Professional version, which gets you the climate data in addition to a bunch of other really useful tools.  The cost of the upgrade is significantly less than if you were to purchase Akton psych chart, which is what is driving the PEC version.   This link jumps you to the portion of the blog post that describes the features.

Having said all of that, for this type of calculation, you need to somehow come up with a seasonal assessment of the load profile, which usually is reflected by the flow profile.  Here are some ways I have done that.

Ask the Building

I have asked the building.  For example, if I am trying to understand the load on a chiller plant, if I can come up with a way to document the distribution system flow rate and temperature rise, then I can use the water side load equation (to the left) to come up with the load profile. 
 Of course, if I can measure the flow, then that is all I need to apply the affinity law.  But flow meters are not all that common in legacy systems, and sometimes, you don't have the luxury of a portable, strap-on flow meter.  In those situations, I have used a number of tricks.

For a primary/secondary system, you may be able to monitor chiller temperature drop and use pump tests to establish the flow rate through the chillers, which should be (by design) relatively constant in this sort of system.  That information allows you to come up with the tonnage profile.

Then, you apply the conservation of mass and energy principle.  More specifically, you log differential temperature across the distribution system.  Then, since the tons produced by the chillers are the tons consumed by the distribution network, you solve the water side load equation for flow and use the chiller tons along with the logged distribution system temperature rise to calculate the flow in the distribution system.
 Logging differential pressure is usually a lot easier than logging flow.  So, if you can log differential pressure across something like a circuit setter in a pumping system, you can then use the differential pressure along with the circuit setter flow vs. differential pressure curve to calculate a flow for each logged interval.  In the image to the left, we used 4-20 ma transmitters wired to a hobo data logger to log differential pressure across a Bell and Gossett circuit setter in a hot water system.  Then, we used the circuit setter flow coefficient - which mathematically relates flow rate with differential pressure - to calculate the flow rate for each differential pressure reading.   The result was a flow profile that we could correlate with the outdoor air temperature that existed at the time.
We could then take that data and use regression techniques (which sounds way more complicated than it is given the trend line feature in Excel) to come up with a relationship between outdoor air temperature and hot water system flow rate.  Once you have that relationship, you can use it with an hourly weather data file or a bin weather data file to calculate the flow rate associated with the outdoor air temperature for each hour or bin in the data set.

Scale a Known Profile to Match the Facility in Question

Sometimes, I have a data set that gives me a flow profile for a very similar system or building in a very similar climate relative to the system I am looking at.  So, to get a sense of what might happen in the facility I am studying, I scale the known data set to match the metrics of the facility I am looking at.

In the images below, the flow profile to the left is a logged flow profile for an office building that had similar occupancy patterns in a somewhat similar climate relative to a new building I was looking at.   To do one of the assessments I wanted to do, I needed some sort of flow profile to work with.  So, I scaled the profile on the left to generate the flow profile on the right based on the maximum system design flow rates.  I also filtered it to eliminate the after hours operation that existed in the original facility.   While not perfect the profile gave me a way to do a rough order of magnitude assessment of some of the options we were considering, which is all I needed for that project.

Use a Recognized Resource Like ASHRAE

Prior to the most recent edition of the ASHRAE Applications Handbook, Chapter 3 - Commercial and Public Buildings included a table that had load profile shapes for typical applications in this category.
To make a first pass assessment for a system that I had little information on, I have used those load profile shapes to establish a flow profile.  For most of our systems, the space load profile is what is driving the flow profile for the air handling systems.

Do a Manual Load Assessment

When I entered the industry, we were still doing loads via manual calculation techniques like the Cooling Load Temperature Differential method (CLTD), which evolved to the Radiant Time Series method (RTS).  You can still find the tables associated with the CLTD method in the ASHRAE Pocket Handbook, at least you can in the 7th edition, which is the latest version that I have.
Once you have been through the process, it does not take a crazy amount of time to do the calculation, especially if you set up a spreadsheet the right way.  Plus, you will learn a lot about your facility by thinking through the calculation.  Here is an example of one I did for one floor in a high-rise I was looking at for a field exercise during a session of the PEC EBCx Workshop class a couple of years ago.
In a similar vein, ASHRAE offers a spreadsheet that will facilitate doing a RTS load calculation for a modest cost;  far less than it would cost you to build your own.  And if you run a load out using it, you will learn a lot if you have never done it before.  If you have done it before, you will still learn a lot about the system you are looking at, which is valuable knowledge.

Recognize that for a 100% Outdoor Air System, the Coil Load is an Outdoor Air Load
Corollary:  Integrated Economizer AHUs are 100% Outdoor Air Systems a Lot of the Time

One thing that is obvious in hindsight but that I didn't fully appreciate earlier in my career is that the load on coils in a 100% outdoor air system is a pure outdoor air load that can be addressed by applying the upper equation for situations where both sensible and latent heat transfer are happening (for instance a, a cooling coil) and by applying the lower equation for situations where only sensible heat transfer is occurring (a preheat coil for instance).

So, for a constant volume system, the load profile can be generated by using these equations and an hourly weather data file or bin weather data with adjustments made to reflect the hours of operation.
For a variable flow system, you will still need to know the flow profile.   If that data is not available via some sort of flow measuring system, one option is to do something similar to what is illustrated above with the circuit setter.   

Specifically, if you log differential pressure across something like a coil and when you deploy the logger, measure the flow rate happening at the time so you can correlate it with the pressure drop at the time, then you can use the logged data and the square law to calculate the flow that exists for each logged differential pressure reading.   If you are using this approach a preheat coil or a series of duct fittings that generate a meaningful pressure drop will be a better choice than a chilled water coil or the filters because the chilled water pressure drop will be different if the coil is wet vs. dry and the filter pressure drop will tend to change as the filters load.  

You can also use fan speed or fan differential pressure, fan speed, or fan amps as a proxy for flow, but you have to make a lot of assumptions to account for how the fan speed is controlled and where the fan is operating on its curve at any given point in time.
 For example, in the constant volume system illustrated to the left, the fan is controlled to maintain a constant flow in the system as the filters load up.  So, with clean filters (blue lines amd text), the fan speed would be 836 rpm and the power consumption would be about 25 Bhp.   

By the time the filters become  dirty and need changed (red lines and text), the fan speed would have increased to 900 rpm and the power consumption would be about 30.5 Bhp.  So in this case, the change in fan speed and power did not at all reflect a change in flow. 
 In contrast, for the VAV system illustrated to the left, which serves four identical variable volume zones zones, the fan is controlled to maintain a fixed set point at a remote point in the system where the duct splits to serve the four zones.  With all of the zones at full flow, with clean filters (the red lines and text), the fan operates at 836 rpm and consumes about 25 Bhp.

If two of the zones shut down totally, reducing the demand for flow to 50% of design (the yellow lines and text), the fan speed drops to  476 rpm and it 
consumes about 4 Bhp.  So in the second example the change in fan speed does actually correlate to a change in flow and power consumption.   But to accurately characterize flow or power as a function of fan speed, you would need to do an analysis similar to what is illustrated but with enough points to define a relationship over the entire operating range.   This can certainly be done, as illustrated below, where four different operating points were assessed using fan curve analysis techniques (left image) and then the Bhp vs. speed relationship was plotted and fitted with a curve (right image).
The equation for Bhp vs. speed could then be used to calculate Bhp based on logged fan speed data.   But if you had a logger capable of logging coil pressure drop, then that approach would likely take less effort and would also have fewer assumptions in it.

Log Something Measurable as a Proxy for Something Harder to Measure

Steam flow can be very challenging to pick up, even with current technology. Back when I first entered the industry, it was even harder, especially for systems that had high turn-down ratios.   But if you were trying to understand how a steam plant used energy, the information was crucial.   

Very early on in my career, when faced with just such a challenge, Chuck McClure, the founder of McClure Engineering (the firm that took a chance that an Aircraft Maintenance Engineer/A&P Mechanic might work out as an HVAC tech) taught me a really cool trick that I still use.  Basically, he had me wire alarm clocks across the starter coils of the feed water pumps and condensate pumps in the system.  

For the condensate pumps, each time they cycled, the pumped out a known volume of condensate with a very predictable run time.  So if you knew the total run time in a given period, you could divide it by the cycle time and come up with the number of cycles, which you could then convert to a volume of condensate.  Since the condensate was simply the condensed steam,  that information gave you some perspective on the amount of steam used by the area served by the condensate pump, minus any losses due to leakage or direct use of the steam in a process like a steam humidifier.

For the feed water pumps, a similar concept was applied but the run time was related to the operating point on their system curve, which would be fairly constant because they pumped from a tank with a fairly constant level into boilers operating at a fairly constant pressure.  So, if you knew the run time (minutes) and the operating point (gallons per minute) you could calculate the amount of water that went into the boilers to become steam for given interval.   You needed to correct that for any blow down that happened, but that was fairly easy to do by measuring a typical blow down volume and noting how many times that happened during the interval you were studying.

If you want to know more about the technique and how to do it with data loggers, I wrote a string of blog posts titled Assessing Steam Consumption with an Alarm Clock.  My point in bringing it up here is to illustrate how you might be able to come up with a way to measure something simply by thinking out of the box about it, like Chuck did back in 1979.


A Common Affinity Law Misapplication

Frequently, it is assumed that if there are two fans or pumps in parallel serving a load, the, via the cube rule, significant energy will be saved by operating both of the fans or pumps together at a lower speed as compared to operating a single fan or pump at a higher speed to serve the same load.  And while this is true for some very specific cases (parallel independent cooling tower cells are a good example), it is generally not true.  

Truth be told, I actually thought this was the case until I had a chance to dig into it while working as a Facilities Engineer at Komatsu.  For reliability purposes, we changed how we operated some of our process exhaust systems from running one fan at full speed and then switching to the other fan if the lead fan failed to running both fans at part speed all of the time. 

This changed allowed the second fan to quickly pick up the load with a relatively minor, very short term reduction in flow if the other fan failed.  This minimized disruption in the clean room when a such a failure occurred  because there never was a loss of process exhaust flow.  In contrast, the time lag associated with detecting a fan failure and starting the back-up fan usually triggered a fab evacuation because of the loss of process exhaust flow that would occur during the transition.

At the time we made the change, I thought it would also save energy due to the "cube rule".  But that turned out not to be the case, and I finally figured out why.
If you consider the fan kW equation to the left the amount of work you are doing in a given system is basically a function of the flow and static pressure;  i.e. the mass in motion.   Those values in and of themselves are independent of whether you use one fan or two fans or ten fans to  generate the flow and pressure.

What changes with the number of fans are all of the efficiency factors in the denominator of the equation.   So, if you are using two identical, well selected fans in parallel, either one of which could handle the load and instead operating them together at a reduced speed to handle the load, you likely shift their operating point to a very inefficient point on their curve 
because you cut the flow in half but do not reduce the pressure it needs to be required.   

In other words, you move horizontally across the fan curve at the design operating pressure to a flow rate that is half of the design flow rate, which changes the efficiency that the fan will achieve as the speed drops since the system curve through the new operating point will be to the left of the original system curve.   

As a result, even though the speed reduction will tend to preserve the efficiency that the wheel would have when operating at full speed on the new 50% of design flow system curve (the section above about The Relationship Between Flow and Impeller Speed provides more insight into this) that efficiency will probably be less than it was for the original 100% of flow design system curve unless the original selection was way to the right of best efficiency.  So most of the time, in this situation, the fan (or pump) efficiency will be less than it was for the design condition, meaning you will use more, not less energy with the two fans (or pumps) running to provide the same amount of flow and pressure that one could provide on its own at a higher speed, better efficiency operating point.

Similar shifts in efficiency will happen with the motor and variable speed drive and will tend to result in an over-all increase in energy consumption in this scenario.  And the pressure drop characteristics of the system can change slightly too due to the flow splitting between pumps vs. running through one, and that actually can change the head required just a bit, usually adversely.

That said, if you have one independent cooling tower cell that is operating its fan at full speed and bring a second independent cell on line and divert half of the flow and load to it, then you will actually save quite a bit of energy.  That is because cooling tower capacity is nearly linear with the air flow through the tower.  So, if you reduce the load on a cell to 50% of what it was by sharing it with a second independent, identical cell, both cells together will be able to serve the load by running their fans at 50% speed or 1/8 of the full speed power (1/2 times 1/2 times 1/2; i.e. 1/2 cubed).

As a result, the fan energy drops to 1/4 of what it was (two fans operating at 1/8 of full speed power).   The words "independent cooling tower cell" is the key to why this works.  If the cells are independent, then from a fan kW standpoint (the equation above) you have doubled the fill cross sectional area;  each cell is handling half of its design air flow rate.  If the air flow rate is 50% of design, the pressure drop through the fill will be 25% of design and the fan power will be 12.5% of design.

The caveat' is that the water flow has to be distributed uniformly across the fill for this to work.   Otherwise, some of the fill will run dry, short circuiting the air flow and raising the fan power above what would be predicted by the math.  This can also ruin the fill because it will tend to scale in the areas where the water evaporates from it before reaching the cold basin.   If you want to know more about this, you will find additional information in the blog post titled Cooling Tower Flow Distribution and Variable Flow in Condenser Water Systems.  You will find videos that demonstrate what can go wrong on the Cooling Tower Flow Variation videos page of this web site.

Time precludes providing additional detail at this point, but eventually I will develop a blog post about this fallacy.  Meanwhile, the PowerPoint presentations below will provide some additional detail to help you understand things a bit more.  They use parallel pumps to illustrate the phenomenon, but the same concepts can be applied to parallel fans.
Parallel Pumps and Affinity Laws.pdf
File Size: 2817 kb
File Type: pdf
Download File
Parallel Systems and Affinity Laws.pdf
File Size: 1138 kb
File Type: pdf
Download File

Home

Blog

Contact
Picture
A Field Perspective on Engineering - © 2017 Facility Dynamics Engineering, All Rights Reserved
(Contact Me to Check on Lefts or Any Other Questions You May Have about Permissions)